在行测复习过程中,大部分考生都在对一个部分非常头疼,那就是数量关系。一拿到题目不知道该从什么地方入手,不知道该用什么方法去解题。
那么数量关系的知识点到底是什么呢,其实我们公务员考试当中的数学知识有很大一部分只是小学的数学问题,那有考生就更有疑问了,那我为什么还是做不出来呢,有最主要的原因就是不知道用什么方法,今天给大家带来用几种不同的方法解题。
【例1】 某高校组织省大学生运动会预选赛,报名选手中男女人数之比为4∶3,赛后有91人入选,其中男女之比为8∶5。已知落选选手中男女之比为3∶4,则报名选手共有:
A. 98人 B. 105人
C. 119人 D. 126人
【答案】C
【解题思路】
1.方程法
第一步,设男选手人数为4x,则女选手人数为3x,总选手数为7x。
第二步,赛后有91人入选,其中男女比例为8:5,则入选的人中有56人为男选手,35人为女选手。那么落选的男选手有(4x-56)人,落选的女选手有(3x-35)人,落选的男女之比为3:4,可列方程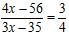 ,十字相乘得16x-224=9x-105,化简得7x=119,则报名选手共有119人。因此,选择C选项。
,十字相乘得16x-224=9x-105,化简得7x=119,则报名选手共有119人。因此,选择C选项。
十字交叉法:十字交叉解题,所有报名选手中男选手占4/7,其中入选的男选手占8/13,落选的男选手占3/7,那么十字交叉结果如下,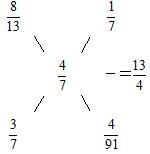 。可得入选选手和落选选手人数之比为13:4,那么报名的选手共有91÷13×17=119(人)。因此,选择C选项。
。可得入选选手和落选选手人数之比为13:4,那么报名的选手共有91÷13×17=119(人)。因此,选择C选项。
【例2】某单位举行象棋比赛,计分规则为:赢者得2分,负者得0分,平局各得1分,每位选手与其他选手各下一局。已知男选手数是女选手的10倍,而得分是女选手的4.5倍,则参加比赛的男选手数是:
A. 40人
B. 30人
C. 20人
D. 10人
【答案】D
【解题思路】
1.带入排除法
第一步,题目难度较大,无从入手,考虑使用代入排除法解题,代入验证时采用就简代入原则,优先从D选项10开始代入。![]()
第二步,若参加比赛的男选手为10人,则参加比赛的女选手为1人,共11人。每场比赛无论是分出胜负还是平局,均共得2分,11人参加循环赛共进行=55场比赛,得分总数应该为55×2=110分,男选手得分是女选手的4.5倍,则女选手共得110÷5.5=20分。1名女选手共参加10场比赛,如果都获胜恰好得20分,满足题意。因此,选择D选项。
2.方程法
设女选手有x人,则男选手有10x人,共有选手11x人。进行循环赛共有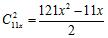 场,每场比赛无论是分出胜负还是平局,均共得2分,因此循环赛总分数为(121x2-11x)分。男生所得分数是女生的4.5倍,则女生所得分数为
场,每场比赛无论是分出胜负还是平局,均共得2分,因此循环赛总分数为(121x2-11x)分。男生所得分数是女生的4.5倍,则女生所得分数为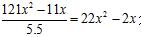 分。一个女生共进行11x-1场比赛,最多得22x-2分,则22x2-2x≤22x-2,解不等式得x≤1,则最多有1名女选手,10名男选手。因此,选择D选项。
分。一个女生共进行11x-1场比赛,最多得22x-2分,则22x2-2x≤22x-2,解不等式得x≤1,则最多有1名女选手,10名男选手。因此,选择D选项。











